本文通过一个简易浅显的项目阐述几种复杂网络中常用的社区发现算法，github地址：

网络中节点1，2，3，4都是用户，用户之间可能互相给对方发数据，每个人发不发和给谁发都是随机。 假设我们认为谁收到的数据最多为胜者，那这个时候可能存在作弊的用户。 一些作弊用户使用同一个ip地址通过一直互相发数据来取得比赛胜利。

解题思路如下： 构建两个网络A，B，网络A以发数据作为edge，网络B以相同IP作为edge。 即网络A中，edge的两端是发送方和接收方的关系，而在网络B中，edge的两端是两个IP相同的用户。 根据community detection的思路，网络A的community是那些发数据较为频繁的用户集合，网络B中的community是IP较为集中的用户集合。 如果A和B中community的重合率很高的话，那么它们就有可能是作弊用户。

通过NetworkX构建有向图，那么网络A中edge的属性应该为count（连接次数）和amount（金额）。 网络B中应该不带任何属性，只要两个节点曾经用过相同的IP，那么两者之间即有一条edge。 利用NetworkX构建多重有向图，发送次数通过计算边的重数可得。 构造网络具体说明：

• 网络A（多重有向图）的节点为各用户，如果用户1以IP（255.255.255.0）向用户2发送金额为30的数据，那么添加一条有向边（用户1→用户2），边强度为30。
• 网络B（多重无向图）的节点为各用户，如果用户1以IP（255.255.255.0）向其他用户发送了5次数据，用户2以同样IP（255.255.255.0）向其他用户发送了2次数据，那么添加一条无向边（用户1—用户2），边强度为min（5,2）=2。

• 算法原理

对于一个图G而言，如果其中有一个完全子图（任意两个节点之间均存在边），节点数是k，那么这个完全子图就可称为一个k-clique。

进而，如果两个k-clique之间存在k-1个共同的节点，那么就称这两个clique是“相邻”的。 彼此相邻的这样一串clique构成最大集合，就可以称为一个社区（而且这样的社区是可以重叠的，即所谓的overlapping community，就是说有些节点可以同时属于多个社区）。 下面前两张图表示两个3-clique形成了一个社区，第三张图是一个重叠社区的示意图。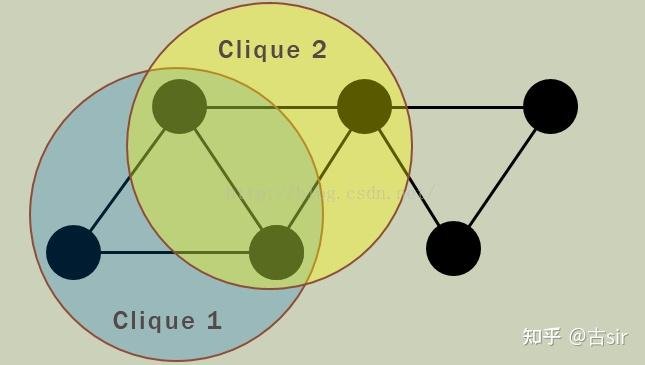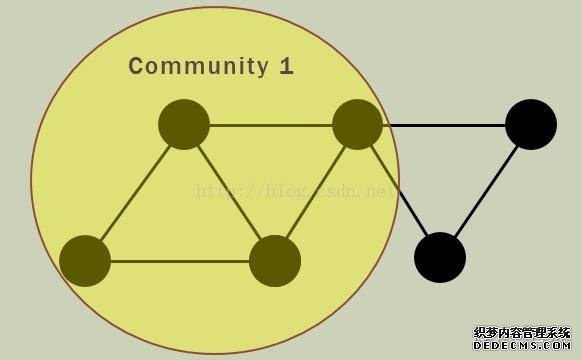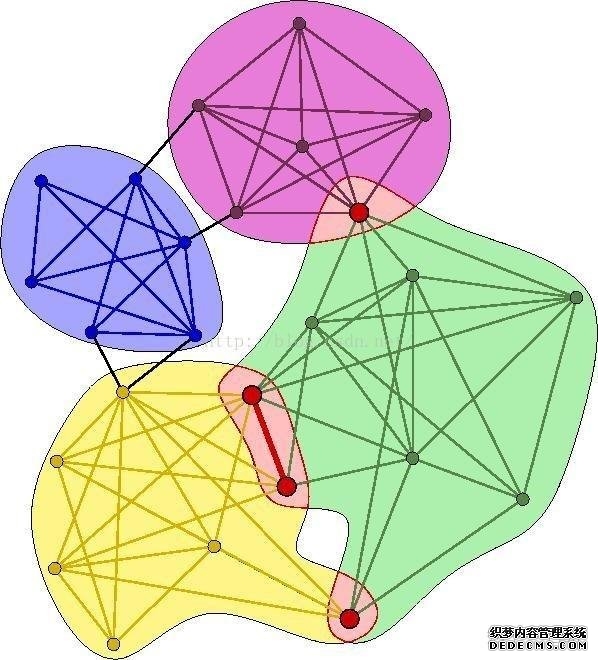

在NetworkX中可以直接调用clique渗透算法（且是唯一一个用于社区发现的算法），使用文档如下：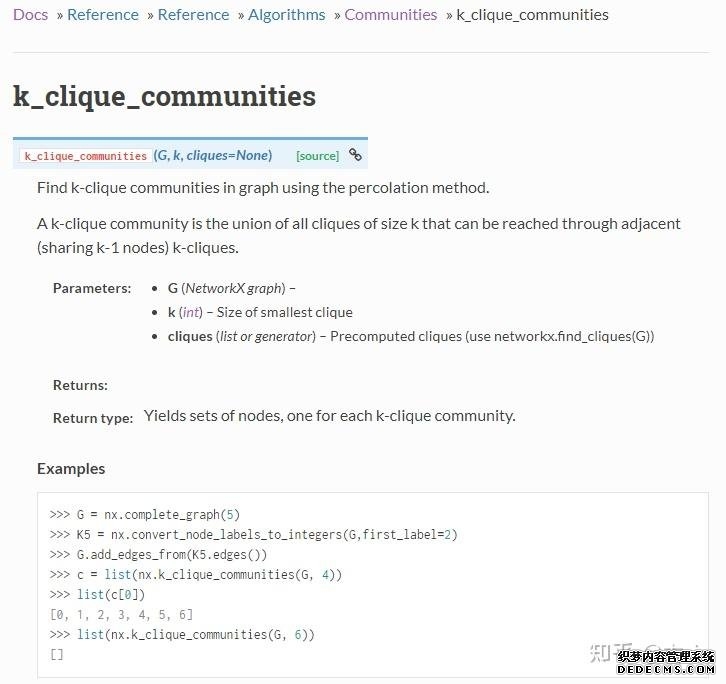

• 利用clique渗透算法构建网络A和B

a. 构建网络A

从自己构造的数据集里构造网络A（其中用户1,2,3,8是作弊团伙）：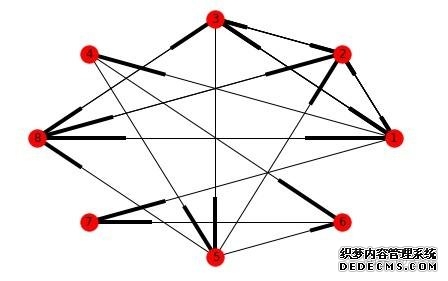

利用clique渗透算法求出网络A中有一个community（紫色）：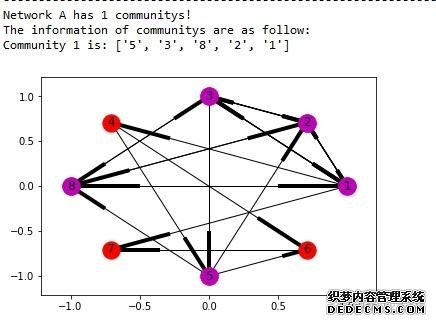

b. 构建网络B

网络B不能直接通过数据集的数据构建，需要进行预处理，首先求出使用相同IP发送数据的用户集，统计结果如下：

构建的网络B如下：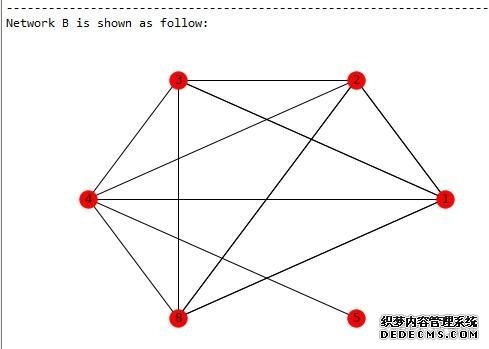

利用clique渗透算法求出网络B中有一个community（青色）：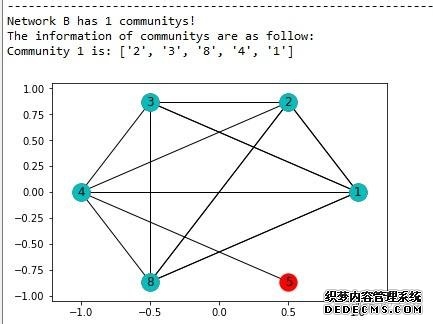

最后求网络A和B中community交集（覆盖率>80%）：

• 算法原理&实验结果

前面主要的工作是对数据集（其中用户1,2,3,8是作弊团伙）分别构建了网络A和B，再利用 networkX 自带的 clique 算法发现网络中的社区， 其中网络 A 只有一个 community[1,2,3,5,8]，网络B也只有一个 community[1,2,3,4,8]，最后通过求交集（覆盖率>80%），求得可疑用户组为 [1,2,3,8]。

接着学习另一个比较出名的社区发现算法：Louvain 算法，这个算法可以根据 edge 的权重进行社区构建，首先构建多重有向图 A，这个和之前方法一致：

但需要注意的是，不论是 clique 算法，还是 Louvain 算法，都只能处理无向图， 所以需要把A转换成无向图，其中A中edge权重设定为节点间的连边数，最后利用 Louvain 算法得出A中的 community：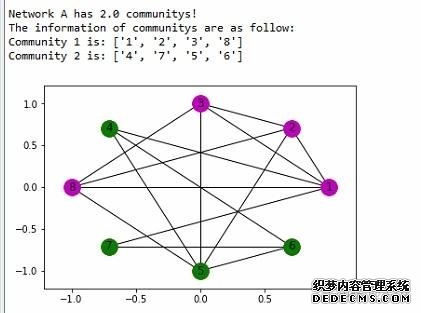

可以看出，利用 Louvain 算法构建网络A时就已经把作弊团伙精确识别出来了(Community 1)，接着构建网络B（如果两点间曾经共用过一个IP，那么则有一条edge）：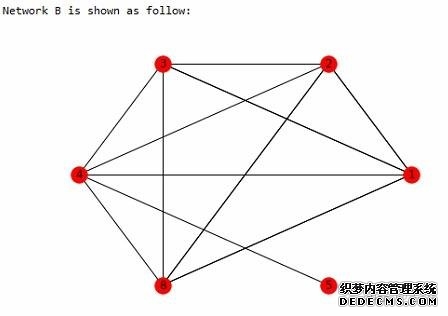

网络B中权重设定如下：假设 A，B 两个用户，曾有IP1和IP2发送过数据，其中IP1的次数为x1,IP2的次数为x2，那么 AB 间的 edge 的权重为：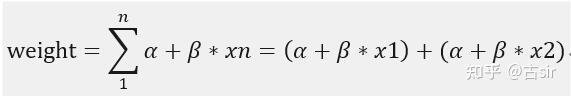

其中 α 和 β 为参数，式子的意义在于权重不仅考虑 A，B 两个用户曾用过几个IP地址，而且将用过 IP 的次数也考虑进权重（实验中 α=2，β=0.5）， 最后利用Louvain算法得出B中的community：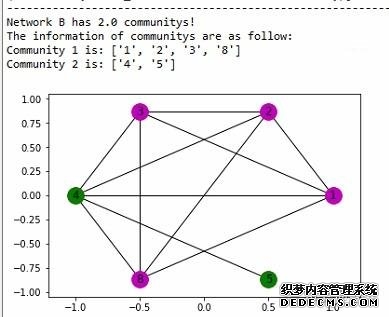

最后求网络A和B中community交集（覆盖率>80%）：

• 结论

从实验效果中看，Louvain 算法比 clique 渗透算法性能要好，划分准确度更高，重要的原因是 Louvain 算法考虑进了 edge 的权重， 但是也有不足的地方，就是这些算法都没有考虑有向图的情况。 但是经过反思，虽然使用算法之前，都将有向图转换为了无向图，但是影响不会很大，因为网络B是根据相同的发送IP进行构建的，虽然是无向图， 但是这个发送IP的属性其实已经暗含了方向性，所以最后的结果也是不错的。

• 算法原理

GN算法中两个重要概念的定义：

• 边介数：所有节点对之间的最短路径中经过该边的最短路径数，边介数大的边往往是连接不同community之间的边。
• 模块度：目前常用的一种衡量网络社区结构强度的方法，可以用来定量的衡量网络社区划分质量，其值越接近1，表示网络划分出的社区结构的强度越强，也就是划分质量越好。 因此可以通过最大化模块度Q来获得最优的网络社区划分。

GN算法伪代码如下：

1) 计算当前网络的边介数和模块度Q值，并存储模块度Q值和当前网络中社团分割情况；
2) 除去边介数最高的边；
3) 计算当前网络的模块度Q值，如果此Q值比原来的大，则将现在的Q值和网络中社团分割情况存储更新，否则，进行下一次网络分割；
4) 所有边分割完毕，返回当前的模块度Q值和community分割情况。

• 实验结果

a. 网络A中聚类结果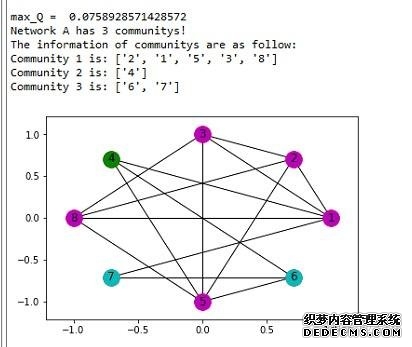

b. 网络B中聚类结果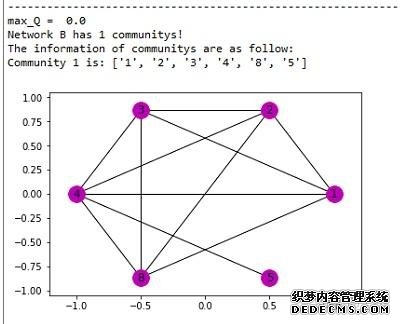

c. 最后的交集结果

• 结论

可以看到GN算法准确性不如之前，识别出来的作弊用户中，用户5被误分为作弊用户，而且GN算法复杂度较高，每次寻求最佳社区分块时，都需要计算每个点之间的最短路径。 不过GN算法也考虑了边的权重（根据模块度进行更新），所以当处理更为复杂网络的时候，GN算法比k-clique算法更为有效。